
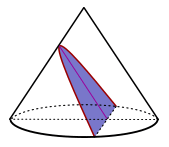
Quando um cone reto é interceptado por um plano paralelo à geratriz do cone, o resultado é uma parábola. Este fato já era conhecido pelos gregos e foi estudado por Apolônio. Tem sido útil para explicar a trajetória de projéteis, para prever quanto tempo levará para um corpo cair em queda livre e, na economia, é usado para descobrir quando um rendimento máximo ou um custo mínimo é atingido. A parábola também foi trabalhada no projeto de radiotelescópios e aquecedores solares.
Dada uma reta \(\mathcal{L}\) no plano, que chamaremos de Diretriz da Parábola e um ponto \(F\) fora da diretriz, que chamaremos de Foco; a parábola com foco em \(F\) e diretriz \(\mathcal{L}\), é o lugar geométrico dos pontos no plano cuja distância ao ponto F é igual à distância deles à diretriz, ou seja:
\(PF = d\left( {\mathcal{L},P} \right)\)
O Eixo Focal da parábola é a reta perpendicular à diretriz \(\mathcal{L}\) e passando pelo foco \(F\).
Dada uma diretriz \(\mathcal{L}\) e um foco \(F\) de uma parábola podemos construir vários pontos que pertencem a esta parábola; para fazer isso, basta realizar as seguintes etapas.
Situação inicial
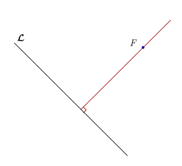
Desenhe o eixo focal da parábola, ou seja, um perpendicular à diretriz \(\mathcal{L}\) e passando pelo foco \(F\).
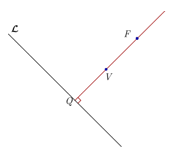
Seja \(Q\) a interseção do eixo focal com a diretriz. Temos que o ponto médio do segmento \(\overline {QF} \) é um ponto da parábola que chamaremos de Vértice da parábola e o denotaremos por \(V.\)
Vários pontos são colocados no eixo focal: \({A_1},\;{A_2},\;{A_3},{A_4}\), etc. Através deles são traçadas linhas paralelas à diretriz. É conveniente que um desses pontos seja o foco da parábola.
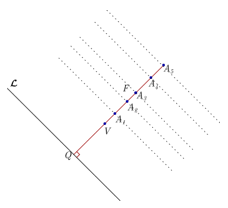
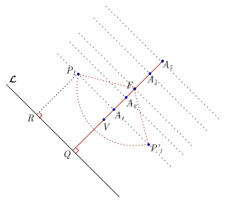
Com o compasso, desenhe um arco de circunferência com centro no foco \(F\) e raio \(Q{A_1}\); as interseções do arco recém traçado com a reta paralela à diretriz que passa por \({A_1},\) são pontos da parábola com foco em \(F\) e diretriz \(\mathcal{L}\).
Temos que \(F{P_1} = Q{A_1}\) e o quadrilátero \(RQ{A_1}{P_1}\) é um retângulo para o qual \(R{P_1} = Q{A_1}\):
\(d\left( {\mathcal{L},{P_1}} \right) = R{P_1} = QA\_1 = F{P_1}\)
De onde se conclui que o ponto \({P_1}\) é um ponto da parábola com foco em \(F\) e diretriz \(\mathcal{L}\).
Com o compasso, desenhe um arco de circunferência com centro no foco \(F\) e raio \(Q{A_2}\); as interseções do arco recém traçado com a reta paralela à diretriz que passa por \({A_2},\) são pontos da parábola com foco em \(F\) e diretriz \(\mathcal{L}\)
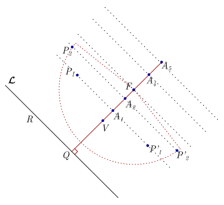
O mesmo procedimento é seguido para os outros pontos no eixo focal.
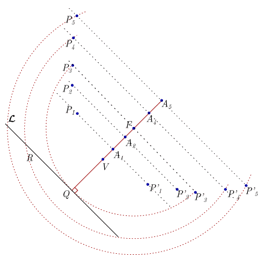
Juntando os pontos obtém-se o contorno de uma parábola

A figura a seguir mostra outros elementos importantes da parábola, além do foco, diretriz e eixo focal.

Um segmento que une dois pontos de uma parábola é chamado de corda, como o segmento \(\overline {AB} ,\;\) uma corda que passa pelo foco da parábola é chamada de corda focal, como o segmento \ ( \overline {CD} \) e a corda focal que é perpendicular ao eixo focal é chamada de lado reto da parábola, neste caso é o segmento .
Denotaremos com \(p\) o comprimento do segmento \(\overline {VF} \), ou seja:
\(p = FV.\)
Com o exposto teremos o seguinte
\(d\left( {\mathcal{L},P} \right) = QF = 2VF = 2p\)
\(RR’ = 2FR = 2FQ = 2\left( {2p} \right) = 4p\)
Isso estabelece que o comprimento do lado de uma parábola é igual a quatro vezes a distância do foco ao vértice, equivalente a duas vezes a distância entre o foco e a diretriz da parábola.
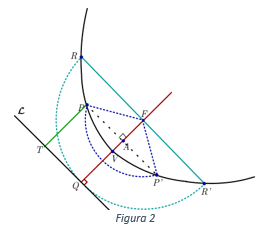
Os pontos \(P\) e \(P’\) são pontos da parábola e o ponto \(A\) é o ponto médio do segmento \(\overline {PP} \)’, o exposto acima nos leva a concluir que \(P\) e . Eles são simétricos em relação ao eixo focal da parábola. Como o acima ocorre para todos os pontos da parábola, podemos concluir que a parábola é simétrica e seu eixo de simetria é seu eixo focal.
Para fins de projeto, basta estabelecer previamente a posição do foco e do vértice para definir todos os pontos da parábola. A Figura 3 mostra uma das características da parábola usada no projeto de radiotelescópios e fogões solares.

Quando um raio atinge um objeto em forma de parábola e o faz de forma que segue uma trajetória paralela ao eixo do foco, ele será refletido de forma que passe pelo foco. Devido a essa propriedade, os radiotelescópios têm formato parabólico porque os sinais se concentram no foco e por isso é o local apropriado para a antena receptora. Algo semelhante acontece com um fogão solar, onde os raios do sol se concentram no foco.
Da mesma forma, se um farol tiver uma forma parabólica, ao colocar uma fonte de luz no foco da parábola, eles serão refletidos de tal forma que os raios sairão paralelos ao eixo focal.

Artigo de: Marco Antonio Rodríguez Andrade. Graduado em Física e Matemática, com mestrado em Matemática, ambos pela ESFM, e doutorado em Ciências pela UNAM.
Referencia autoral (APA): Rodríguez Andrade, M. A.. (Março 2023). Conceito de Parábola (Matemática). Editora Conceitos. Em https://conceitos.com/parabola-matematica/. São Paulo, Brasil.