
Um vetor é um elemento padrão de propriedade visual simbolizado a partir de um segmento de reta orientado (seta), cuja função, na Física, permite apresentar grandezas que possuem magnitude, direção e sentido, como é o caso do deslocamento, da velocidade, da aceleração, da força, do momento estático, do momento angular, entre outras grandezas. No entanto, os vetores não são exclusivos da Física, pois são aplicados também em outras áreas como Álgebra e Geometria, embora geralmente de forma um pouco mais abstrata.
Para representar graficamente os vetores, é necessário o uso de algum sistema de coordenadas como referência para usar a escala para representar sua magnitude, direção e sentido. Na maioria dos casos, o sistema de coordenadas cartesianas é usado, mas outros sistemas, como coordenadas polares, cilíndricas ou esféricas, também podem ser usados.
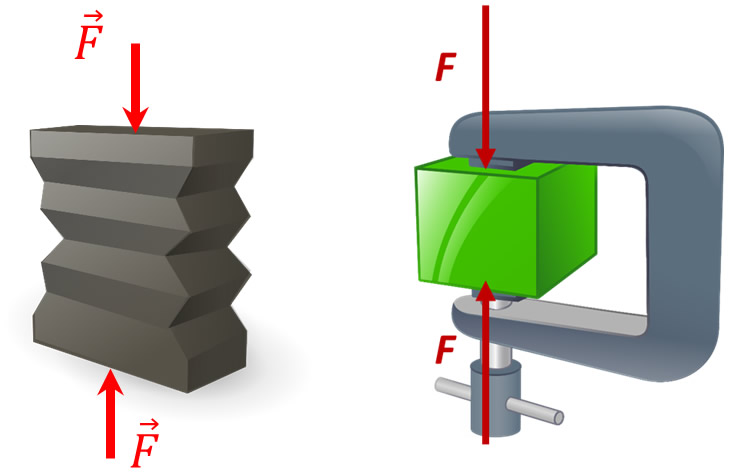
A força é uma grandeza física vetorial
Conforme mencionado, os vetores são representados por uma seta que possui um início, um fim, uma linha de ação e um tamanho:
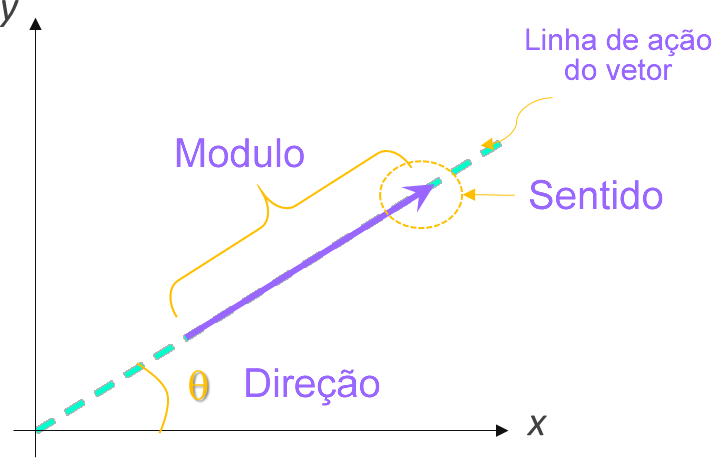
Magnitude: Esta característica também é chamada de intensidade, norma ou módulo, e representa o tamanho do vetor. Esta propriedade é de grande valia para representar outras grandezas físicas, pois mesmo ao medir (por exemplo, com uma régua) o tamanho do vetor a dimensão dessa medida é o comprimento, pode-se definir um equivalente entre esse comprimento e a magnitude da grandeza vetorial a que está associada; digamos, 10 cm → 20 N.
Direção: esta característica expressa a inclinação do vetor em relação a um eixo de referência (geralmente um eixo cartesiano) e é expressa por um ângulo. Quando se deseja representar ou medir graficamente a direção do vetor, utiliza-se um transferidor. Muitos autores costumam expressar a direção de um vetor no plano do eixo horizontal positivo no sentido anti-horário.
Sentido: indica a orientação do vetor, ou seja, para onde aponta a seta. Por exemplo, um vetor pode ter uma direção vertical, mas a direção especifica se é para cima ou para baixo. Analiticamente, quando o vetor é expresso a partir de seus componentes retangulares, o sentido é determinado pelo sentido de seus componentes.
Existem muitos critérios para classificar vetores, incluindo sua relação com outros vetores ou de acordo com uma referência:
• De acordo com a álgebra vetorial, os vetores podem ser:
Paralelos: têm a mesma direção e sentido (não necessariamente a mesma magnitude).

Opostos: Eles têm a mesma magnitude e direção, mas sentido oposto.
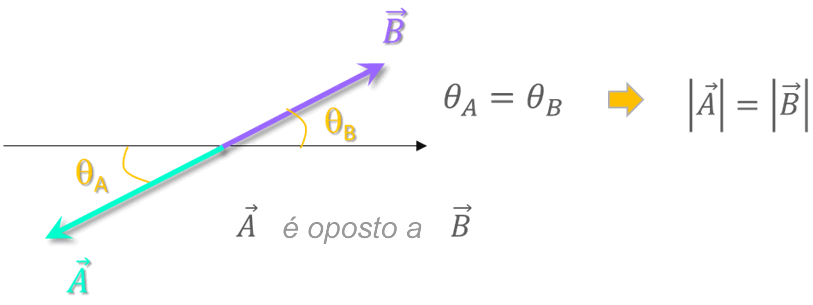
Antiparalelo: eles têm a mesma direção, mas sentido oposto (não necessariamente a mesma magnitude).
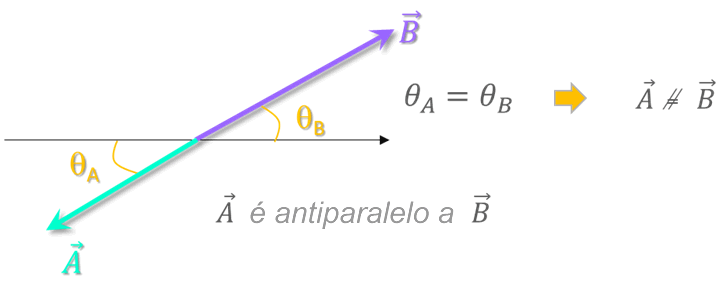
Idênticos: são vetores que possuem a mesma magnitude, direção e sentido. Analiticamente, esta condição implica que os vetores são iguais em todos os seus componentes.
De acordo com suas propriedades de referência:
Livres: são vetores que não estão vinculados a um sistema de referência, de modo que podem ser colocados em qualquer localização espacial e terão o mesmo significado desde que mantenham sua magnitude, direção e sentido. Por exemplo, o vetor momento estático é equivalente a um par de forças, que se comportam como um vetor livre.
Fixos: são vetores que mudam sua localização espacial, modificando o efeito que produzem no sistema. Esses vetores estão ligados a um sistema de referência.
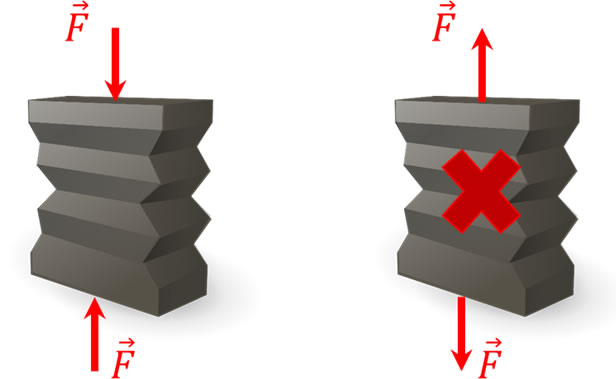
Ao mudar a localização das forças, o efeito sobre o corpo deformável é modificado, pois o efeito de compressão é diferente do efeito de tração.
Deslizantes: são vetores que só podem ser movidos ao longo de sua linha de ação. Por exemplo, quando as forças atuam sobre corpos rígidos, elas se comportam como vetores deslizantes, o que significa que independentemente de onde sejam representadas ao longo de sua linha de ação, sempre terão o mesmo efeito e resultado no sistema.
De acordo com a referência, os vetores podem ser fixos, livres e deslizantes.
De acordo com seu valor ou aplicação:
Vetor nulo: é um vetor cuja magnitude é zero e com direção e sentido arbitrários. A definição deste vetor surge da necessidade de justificar a subtração entre dois vetores idênticos, pois por definição, o resultado da subtração de dois vetores deve ser também um vetor.
Vetor unitário: é um vetor adimensional cujo módulo é igual à unidade. Este vetor é muito útil em operações vetoriais para expressar outros vetores, pois ao multiplicar um escalar por um vetor unitário, isso lhe dá a direção e o sentido para que o resultado seja um vetor com a magnitude do escalar e a direção e sentido unitário.
Vetor de posição: é um vetor que é usado para expressar a localização de um ponto no espaço. Vai desde a origem do sistema de referência até o ponto de localização da partícula.

Artigo de: Evelyn Maitee Marín. Engenheira industrial com mestrado em Ciências Físicas Aplicadas e doutorado em Ciências da Educação. Professora universitária.
Referencia autoral (APA): Marín, E. M.. (Agosto 2023). Conceito de Vetor. Editora Conceitos. Em https://conceitos.com/vetor/. São Paulo, Brasil.