
A trigonometria é um ramo da geometria e da matemática que trata do estudo dos triângulos, bem como das relações existentes entre seus lados e seus ângulos. O triângulo é uma figura geométrica que por centenas de anos intrigou diversas civilizações, a ponto de ser considerado por muitos uma figura perfeita. O desenvolvimento da trigonometria é o culminar de vários séculos de estudo dessas figuras geométricas. Embora à primeira vista pareça que a trigonometria se limita à abordagem dos triângulos, a verdade é que os conceitos que ela aborda têm aplicações em muitas áreas do conhecimento humano. A trigonometria é usada na medição de distância, análise de sinal, modelagem matemática, etc.
Para falar sobre trigonometria, talvez devêssemos começar com a análise do triângulo retângulo. Um triângulo retângulo é um tipo de triângulo que se caracteriza por ter um ângulo reto, ou seja, um ângulo de 90°.
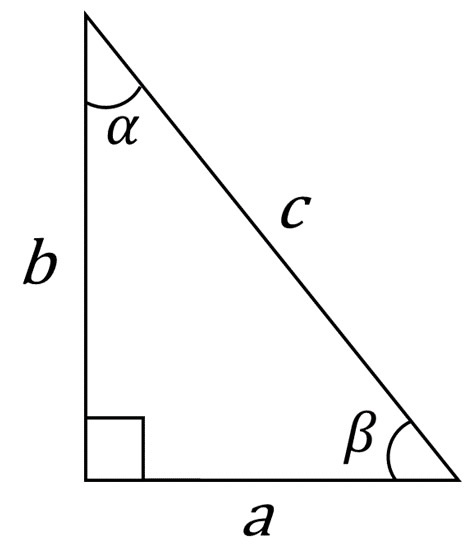
Neste triângulo retângulo, os lados a e b cuja união forma o ângulo reto são conhecidos como “catetos”, o lado restante e que é oposto ao ângulo reto é chamado de “hipotenusa”. Existe uma relação matemática entre os três lados do triângulo retângulo, que estabelece que:
c² = a² + b²
Este é o conhecido “Teorema de Pitágoras”, que nos diz que “em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos”.
O triângulo retângulo e as funções trigonométricas
Do estudo dos triângulos retângulos surgem também as “Razões Trigonométricas” que relacionam os ângulos de um triângulo retângulo com seus catetos e sua hipotenusa. As três principais razões trigonométricas são o “seno”, o “cosseno” e a “tangente”. Essas razões trigonométricas para o ângulo \(\alpha \) do triângulo da figura anterior serão dadas por:
\(\sin \alpha = \frac{a}{c},\;\;\cos \alpha = \;\frac{b}{c},\;\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{a}{b}\)
Por sua vez, essas mesmas razões trigonométricas para o ângulo \(\beta \) seriam:
\(\sin \beta = \frac{b}{c},\;\;\cos \beta = \;\frac{a}{c},\;\;\tan \beta = \frac{{\sin \beta }}{{\cos \beta }} = \frac{b}{a}\)
Existem também outras razões trigonométricas que dependem das acima descritas e são chamadas de “cossecante”, “secante” e “cotangente”. Essas razões trigonométricas para o ângulo \(\alpha \) seriam dadas por:
\(\csc \alpha = \frac{1}{{\sin \alpha }} = \frac{c}{a},\;\;\sec \alpha = \frac{1}{{\cos \alpha }} = \frac{c}{b},\;\;\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{b}{a}\)
Todas essas razões trigonométricas relacionam os ângulos de um triângulo retângulo com quocientes entre seus lados, porém, podemos estender a definição dessas razões a todos os números reais e definir as “funções trigonométricas”.
A variável independente de uma função trigonométrica é um ângulo em radianos, onde 1 radiano é o ângulo compreendido por um arco de circunferência cujo comprimento é igual ao comprimento do raio e tem um valor de aproximadamente 57,3°. O valor de uma função trigonométrica em um determinado ponto é o valor que a razão trigonométrica correspondente teria para aquele ângulo em radianos.
Funções trigonométricas inversas
A princípio, as razões trigonométricas são muito úteis porque, graças a elas, podemos determinar as medidas dos ângulos de um triângulo retângulo se conhecermos as medidas de seus lados e vice-versa.
Existem funções que são inversas às funções trigonométricas mencionadas acima. As funções inversas podem ser definidas como:
\(Si\;y = \sin x ⟹ x = {\sin ^{ – 1}}y\)
\(Si\;y = \cos x ⟹ x = {\cos ^{ – 1}}y\)
\(Si\;y = \tan x ⟹ x = {\tan ^{ – 1}}y\)
As funções trigonométricas inversas nos dão o valor do ângulo que corresponde a um determinado valor de sua respectiva razão trigonométrica. Por exemplo, suponha que no triângulo anterior não saibamos a medida do ângulo \(\alpha \), esse ângulo pode ser obtido usando as funções trigonométricas inversas, de tal forma que:
\(\alpha = {\sin ^{ – 1}}\frac{a}{c} = {\cos ^{ – 1}}\frac{b}{c} = {\tan ^{ – 1}}\frac{a}{b}\)
Uma das aplicações mais importantes da trigonometria é a medição de distâncias. Um exemplo claro disso foi a façanha do astrônomo e matemático grego Eratóstenes que no século III a.C. percebeu que, durante o meio-dia solar do solstício de verão, os objetos em Siena não projetavam sombra, algo ao contrário do que acontecia em Alexandria nesse mesmo momento em que os objetos sim lançavam sombras. Eratóstenes mediu o tamanho da Terra usando funções trigonométricas, medindo o ângulo em que os raios do sol incidiam sobre Alexandria ao meio-dia solar no solstício de verão e conhecendo a distância entre Alexandria e Siena. Atualmente, a trigonometria também é usada para medir a distância de estrelas próximas por meio do método de “paralaxe estelar”.
As funções seno e cosseno possuem uma peculiaridade, que é o fato de possuírem comportamento periódico, ou seja, seus valores se repetem com certa frequência ao longo de todo o eixo dos números reais. Essa característica das funções seno e cosseno as torna candidatas perfeitas para modelar fenômenos que possuem comportamento oscilatório como ondas, movimento circular, movimento planetário, circuitos de corrente alternada, etc.
Além disso, a trigonometria desempenha um papel fundamental na construção e análise de sinais. Qualquer sinal periódico pode ser decomposto como uma soma de funções trigonométricas e vice-versa. Desta forma, a trigonometria nos ajuda a entender sinais de todos os tipos, desde aqueles usados em comunicações até aqueles gerados por processos eletrofisiológicos em nosso corpo.

Artigo de: Ángel Zamora Ramírez. Licenciado em Física. Cursando Mestrado em Engenharia e Física Biomédica.
Referencia autoral (APA): Zamora Ramírez, A.. (Agosto 2023). Conceito de Trigonometria. Editora Conceitos. Em https://conceitos.com/trigonometria/. São Paulo, Brasil.