
Refração é a mudança na direção de propagação de uma onda quando ela passa de um meio com determinado índice de refração para outro meio com índice de refração diferente.
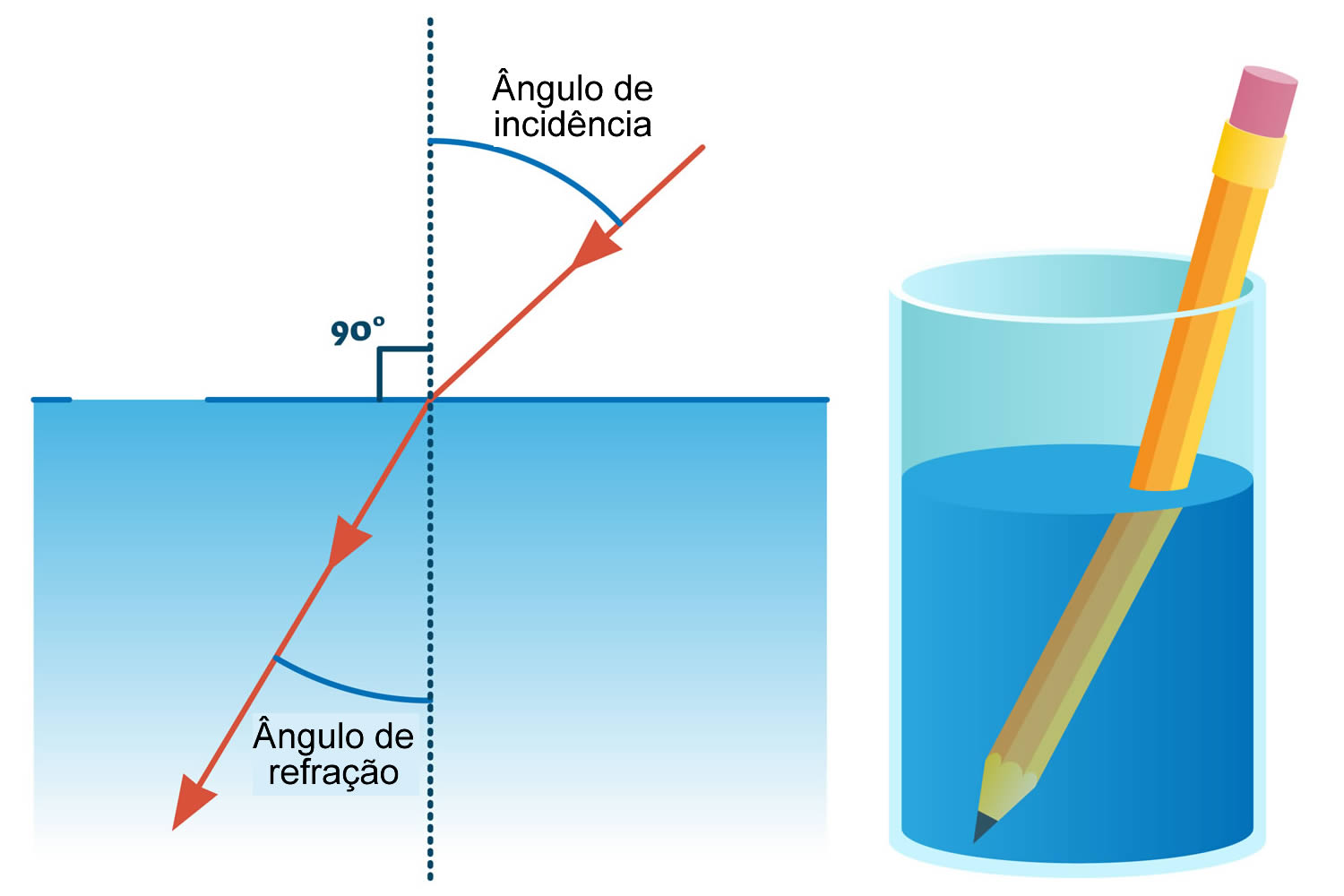
O fenômeno da refração ocorre com diversos tipos de ondas, porém a mais observada é a da luz, como podemos observar quando introduzindo um objeto longo como um canudo em um copo de água. Ao olhar através do vidro parece que o objeto “dobra”, porque a luz refletida pela porção do canudo submersa na água tem uma direção diferente da luz refletida pela porção fora da água. O ar e a água têm índices de refração diferentes, o que cria essa ilusão de ótica.
VectorMine
A velocidade com que a luz se propaga em um meio depende da permissividade elétrica e da permeabilidade magnética do referido meio. No vácuo, a luz se propaga a uma velocidade dada por:
\(c = \frac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}\)
Onde \(c\) é a velocidade da luz no vácuo, \({\mu _0}\) é a permeabilidade magnética do vácuo e \({\varepsilon _0}\) é a permissividade elétrica do vácuo.
Lembrando que a formula acima é validade para o vácuo, mas como é a velocidade da luz em um meio diferente do vácuo? Para fazer isso precisamos usar a permissividade elétrica do referido meio (\(\varepsilon \)) e sua permeabilidade magnética (\(\mu \)). Nesse meio, a velocidade \(v\) na qual a luz se propaga seria:
\(v = \frac{1}{{\sqrt {\mu \varepsilon } }}\)
A relação entre a permissividade elétrica e a permeabilidade magnética desse meio com as do vácuo são as seguintes: \(\varepsilon = {\varepsilon _r}{\varepsilon _0}\), \(\mu = {\mu _r} {\mu_0}\). Onde \({\varepsilon _r}\) e \({\mu _r}\) são a permissividade relativa e a permeabilidade relativa, respectivamente. Substituindo isso na última equação obtemos que a velocidade de propagação da luz naquele meio seria:
\(v = \frac{1}{{\sqrt {{\mu _r}{\mu _0}{\varepsilon _r}{\varepsilon _0}} }} = \frac{1}{{\sqrt {{\mu _r}{\varepsilon _r}} }}\frac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}\)
Este último, usando a definição da velocidade da luz no vácuo (\(c\)), podemos escrever como:
\(v = \frac{c}{{\sqrt {{\mu _r}{\varepsilon _r}} }}\)
Ou também podemos dizer que:
\(\frac{c}{v} = \sqrt {{\mu _r}{\varepsilon _r}} \)
O índice de refração da luz em um meio é definido como a razão entre a velocidade da luz no vácuo e a velocidade da luz nesse meio. Seja \(\eta \) o índice de refração, usando a última equação podemos dizer que:
\(\eta = \frac{c}{v} = \sqrt {{\mu _r}{\varepsilon _r}} \)
Ou seja, o índice de refração de um meio depende de sua permissividade elétrica relativa e de sua permeabilidade magnética relativa. Tanto \({\varepsilon _r}\) quanto \({\mu _r}\) são quantidades adimensionais com valores maiores que 1, portanto \(\eta > 1\). Quanto maior a permissividade relativa e a permeabilidade relativa de um meio, maior será o seu índice de refração.
Foi mencionado anteriormente que quando uma onda como a luz passa de um meio para outro, ambos com índices de refração diferentes, a direção de propagação muda. A lei que descreve este fenômeno é conhecida como “Lei de Snell” e foi formulada pelo matemático holandês Willebrord Snel van Royen. Suponha que temos dois meios com índices de refração \({\eta _1}\) e \({\eta _2}\), um raio de luz viaja através do meio com \({\eta _1}\) e incide no limite de ambos os meios com um ângulo \({\theta _1}\), posteriormente, o raio de luz passa para o meio com \({\eta _2}\) e é refratado com um ângulo \({\theta _2 } \). A lei de Snell postula que:
\({\eta _1}\sem {\theta _1} = {\eta _2}\sem {\theta _2}\)
Ou:
\(\frac{{{\eta _1}}}{{{\eta _2}}} = \frac{{\sem {\theta _2}}}{{\sem {\theta _1}}}\)
Notemos que se \(\theta = 0\) não há refração independentemente dos índices de refração. Além disso, podemos analisar três casos particulares:
Se \({\eta _1} = {\eta _2}\) então \({\theta _1} = {\theta _2}\). Se ambos os meios tiverem o mesmo índice de refração, o raio de luz não muda de direção.
Se \({\eta _1} > {\eta _2}\) então \({\theta _1} < {\theta _2}\). Neste caso, o raio de luz é desviado “para fora” da direção de incidência.
Se \({\eta _1} < {\eta _2}\) então \({\theta _1} > {\theta _2}\). Neste caso, o raio de luz é desviado “para dentro” da direção de incidência.
Talvez muitos de nós conheçamos a capa do álbum “The Dark Side of the Moon” da banda britânica “Pink Floyd”. Esta imagem por sua vez é baseada no famoso experimento de Newton em que ele dispersou a luz branca do Sol com um prisma, obtendo as cores do arco-íris. A luz branca é, na verdade, composta de diferentes frequências, cada uma correspondendo a uma cor no espectro de luz visível. O índice de refração de um meio também depende em parte da frequência da luz incidente.

Blue
Quando um raio de luz branca passa por um prisma, as diferentes frequências que compõem a luz branca experimentam diferentes índices de refração e, portanto, refratam em diferentes direções, desta forma todas essas frequências são dispersas e revelam o espectro da luz visível.

Artigo de: Ángel Zamora Ramírez. Licenciado em Física. Cursando Mestrado em Engenharia e Física Biomédica.
Referencia autoral (APA): Zamora Ramírez, A.. (Setembro 2023). Conceito de Refração. Editora Conceitos. Em https://conceitos.com/refracao/. São Paulo, Brasil.