
A lei de Coulomb é uma lei física que descreve a força elétrica entre duas cargas elétricas em repouso. Foi postulado por Charles Augustin de Coulomb em 1785 e é a base de toda eletrostática. Estávamos no século XVIII quando os fenômenos elétricos estavam sendo desvendados pela ciência. Naquela época já existia a noção de que a matéria possuía uma propriedade conhecida hoje como “carga elétrica” e que dela dependia a interação elétrica que ocorria entre os corpos carregados.
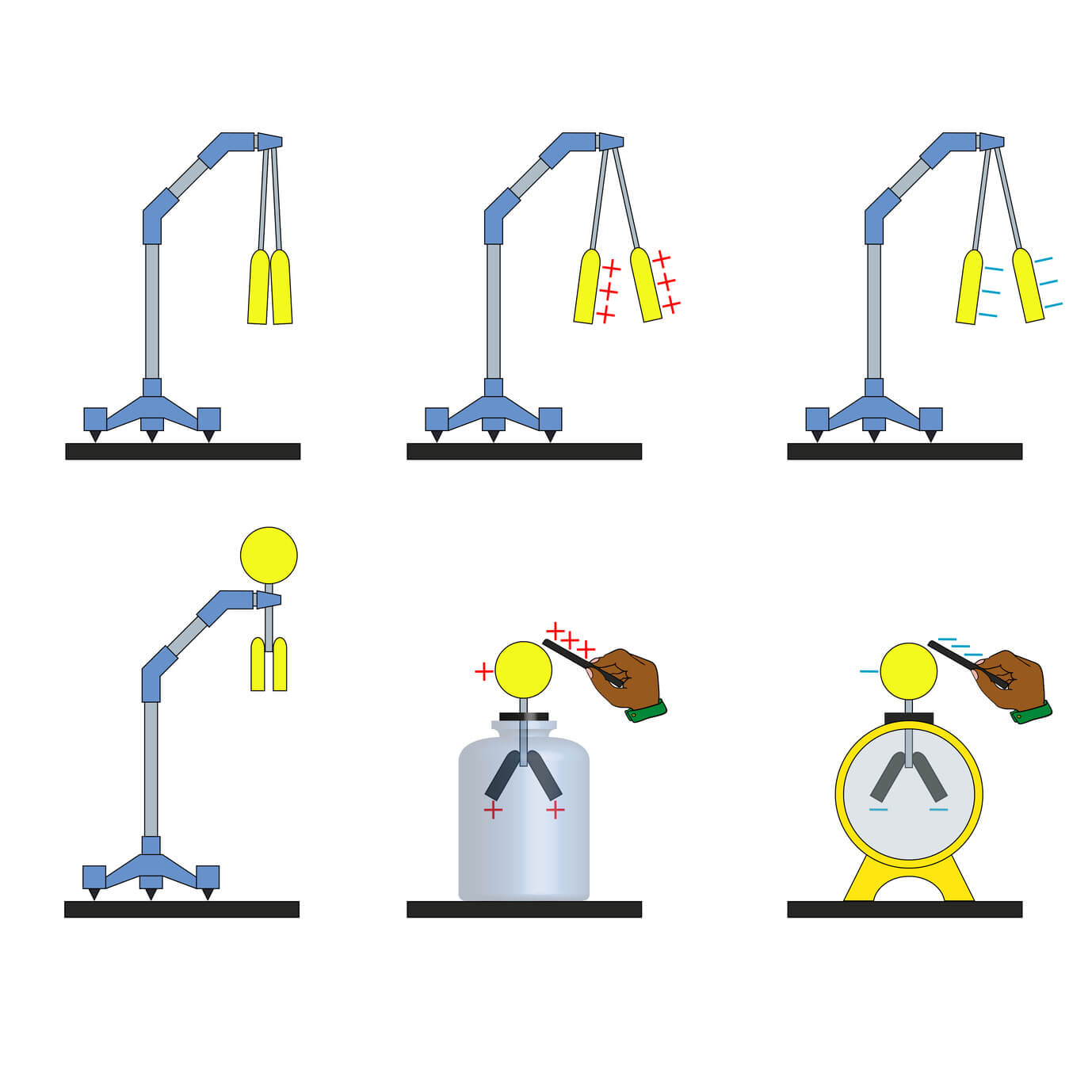
Devemos a maioria das descrições físicas das forças elétricas aos experimentos realizados pelo cientista francês Charles Augustin de Coulomb. Em 1785 Coulomb idealizou um experimento para medir a força entre dois objetos eletricamente carregados: uma balança de torção, inventada por ele mesmo, composta por uma agulha suspensa em uma fina fibra de prata, cobre ou seda.
A agulha tinha uma pequena esfera eletricamente carregada em uma extremidade e um contrapeso na outra extremidade. Quando outra esfera carregada era colocada perto da esfera colocada na agulha, a agulha girava em um plano horizontal devido à interação elétrica entre ambas as esferas, permitindo desta forma, faça medições da força elétrica.
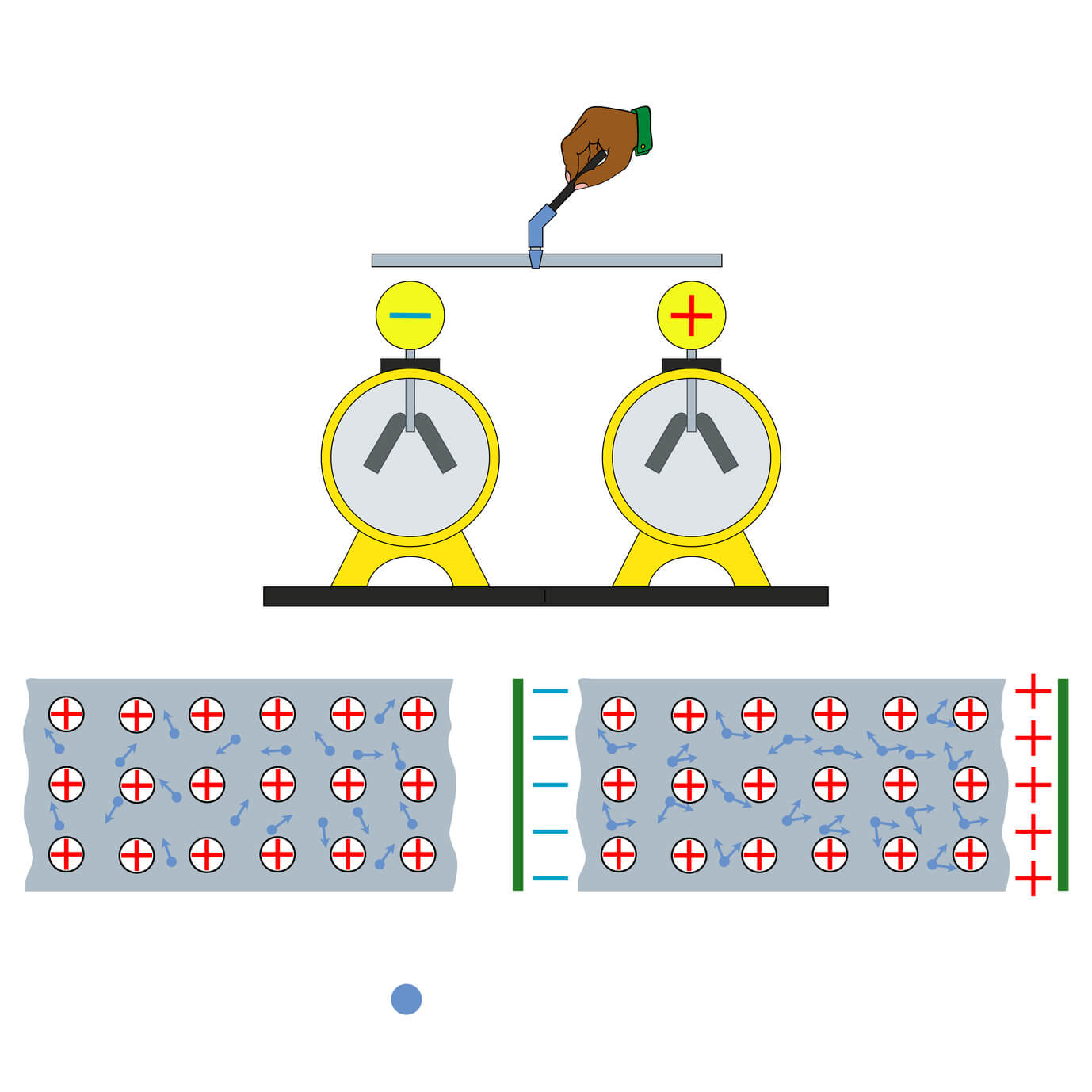
Com estes experimentos, Coulomb formulou sua famosa lei, que em sua versão moderna afirma: “A força elétrica entre duas cargas elétricas em repouso é diretamente proporcional ao produto de ambas as cargas e inversamente proporcional ao quadrado da distância que as separa”.
Sejam \({q_1}\) e \({q_2}\) duas cargas elétricas em repouso e \(r\) a distância que separa ambas as cargas, a lei de Coulomb se parece com:
\(\overrightarrow {{F_e}} = k\frac{{{q_1}{q_2}}}{{{r^2}}}\)
Onde \(k\) é a constante de Coulomb que tem um valor de \(k \approx 8,9875 \times {10^9}\;N \cdot {m^2}/{C^2}\), a direção da força elétrica está ao longo da linha que une ambas as cargas. Nesta equação pode-se notar que se ambas as cargas forem iguais então \(\overrightarrow {{F_e}} > 0\) indicando que a força é repulsiva, enquanto, se uma carga for positiva e a outra negativa, temos que \(\overrightarrow {{F_e}} \lt 0\) o que significa que a força é atrativa.
A lei de Coulomb também pode ser escrita da seguinte forma:
\(\overrightarrow {{F_e}} = \frac{1}{{4\pi {ε_0}}}\frac{{{q_1}{q_2}}}{{{r^2}}}\)
Onde \({ε_0}\) é a permissividade elétrica do vácuo com um valor de \({ε_0} \approx 8,8542 \times {10^{ – 12}}\;{C^2}/N \cdot {m ^ 2}\), poderíamos então dizer que \(k = 1/4\pi {ε_0}\).
Uma característica importante da força eletrostática é que ela satisfaz o princípio da superposição. Se tivermos uma coleção de \(n\) cargas elétricas \({q_1},\;{q_2},\; \ldots ,\;{q_n}\) e uma nova carga \(Q\) for introduzida nesta sistema ), a referida carga elétrica experimentará uma força eletrostática total \(\overrightarrow {{F_T}} \) que é igual à soma das forças individuais devidas a cada uma das cargas que compõem o sistema, ou seja, que : \(\ overrightarrow {{F_T}} = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \ldots + \;\overrightarrow {{F_n}} \), onde \(\overrightarrow { {F_1}} \) é a força exercida pela carga \({q_1}\) na carga \(Q\), \(\overrightarrow {{F_2}} \) a força exercida por \({q_2}\) em \(Q\) e assim por diante.
Isso aqui se torna uma ferramenta muito poderosa porque na maioria dos problemas físicos você não tem cargas elétricas específicas, mas sim grandes coleções de cargas elétricas, de tal forma que se você quiser descobrir a interação elétrica que geraria esse grupo de cargas, basta introduzir uma carga elétrica de teste e somar a força exercida sobre ela por cada carga elétrica do arranjo para finalmente somar todas e obter a força elétrica total.
\(\overrightarrow {{F_e}} = \frac{1}{{4\pi {ε_0}}}\frac{{{q_1}{q_2}}}{{{r^2}}}\)
No entanto, isto só é válido se as cargas elétricas estiverem no vácuo. Se as cargas elétricas estiverem em um meio diferente do vácuo, a força eletrostática \(\overrightarrow {F_e^*}\) entre elas seria:
\(\overrightarrow {F_e^*} = \frac{1}{{4\pi {ε_r} {ε_0}}}\frac{{{q_1}{q_2}}}{{{r^2}}}\)
Onde \({ε_r}\) é conhecido como “permissividade relativa” e cujo valor depende do meio em que as cargas estão imersas. O valor de \({ε_r}\) para vácuo é \({ε_r} = 1\), para outras mídias os valores de \({ε_r}\) assumem valores maiores que 1. Podemos então dizer que:
\(\overrightarrow {F_e^*} = \frac{{\overrightarrow {{F_e}} }}{{{ε_r}}}\)
Como \({ε_r} > 1\) para outros meios que não o vácuo, então o valor da força eletrostática entre duas cargas imersas em um meio é menor que o valor que essa força teria se ambas as cargas estivessem no vácuo. Por exemplo, para água destilada a permissividade relativa assume um valor de \({ε_r} = 80\), isto implica que a força eletrostática entre duas cargas imersas em água destilada é 80 vezes menor do que a força que experimentariam se estivessem em O vazio.
A razão pela qual a força eletrostática entre duas cargas é menor nestes casos é que em um meio diferente do vácuo existem átomos ou moléculas entre o espaço que separa ambas as cargas. Esses átomos ou moléculas também interagem eletricamente de alguma forma "ofuscando" o força elétrica entre ambas as cargas elétricas, o resultado é que a interação entre elas é mais fraca do que se não houvesse átomos ou moléculas interferindo.

Artigo de: Ángel Zamora Ramírez. Licenciado em Física. Cursando Mestrado em Engenharia e Física Biomédica.
Referencia autoral (APA): Zamora Ramírez, A.. (Fevereiro 2024). Conceito de Lei de Coulomb. Editora Conceitos. Em https://conceitos.com/lei-coulomb/. São Paulo, Brasil.