
Expressão matemática que representa o número de vezes que um número A (base) deve ser multiplicado por um número B (expoente) para se obter o número C, formulando a equação: Aᴮ = C. Também, é conhecido como a função inversa à função exponencial.
No entanto, se denomina logaritmo à operação matemática através da qual, dando um número resultante e uma base de potenciação terá que achar o expoente no qual terá que elevar a base para assim conseguir o mencionado resultado. Tal como acontece com a soma e a multiplicação que têm suas operações opostas, a divisão e a resta, o logaritmo tem o expoente como sua função inversa.
Exemplo: 102 = 100, o logaritmo de 100 na base 10 será o 2 e escrevê-lo da a seguinte forma: log10 100 = 2. Este método de cálculo através dos denominados logaritmos foi impulsionado por John Napier no começo do século XVII. O método logarítmico não somente contribuiu para o avanço dá ciência, além disso se transformou numa ferramenta fundamental no âmbito da Astronomia fazendo os cálculos mais simples serem realmente muito complexos. Os logaritmos são muitíssimo usados na geodesia, em alguns ramos da matemática aplicada e na navegação marítima quando as calculadoras e os computadores ainda não eram o fato concreto que são hoje em dia.
Um banco oferece uma taxa anual de 7% de juros compostos ao ano, compostos a cada mês. Em quantos anos o capital investido triplicará?
Solução: Neste caso, a taxa real é (r = frac{{7% }}{{12}}) e (n)
(Cleft( n right) = {C_0}{left( {1 + frac{{0.07}}{{12}}} right)^n})
Onde ({C_0}) é o capital a investir e (n) é o número, substituindo os dados obtemos:
(3{C_0} = {C_0}{left( {1 + 0,0058} right)^n})
(3 = {left( {1.005833} right)^n})
Aplicando o logaritmo a cada membro da expressão anterior:
(log 3 = log left( {{{left( {1.005833} right)}^n}} right))
(0,47712 = nlog left( {{{left( {1,0058} right)}^{}}} right))
(frac{{0.47712}}{{0.0025259}} = n)
(n = 188,89)
A resposta é 188,89 meses o capital vai triplicar, em anos equivale a (15,741).
(0.02551 = log {C_0} + left( {0.002526} right))
Solução alternativa.
Ressalte-se que, nesta solução, trata-se de uma aproximação, e o modelo é viável porque a capitalização é mensal; caso fosse semanal ou diário o resultado seria melhor.
Vamos assumir que é investido a juros contínuos, ou seja:
(Aleft( t right) = {C_0}{e^{rt}})
Onde ({C_0}) é o capital a ser investido, (r) é a taxa anual e (t) é o tempo em anos. Substituindo os dados, obtemos a equação:
(3{C_0} = {C_0}{e^{0.07t}})
(3 = {e^{0.07t}})
Aplicando o logaritmo natural:
(ln 3 = ln {e^{0.07t}})
(ln 3 = 0,07tln {e^{}})
(ln 3 = 0,07t)
(t = frac{{ln 3}}{{0,07}} = frac{{1,0986}}{{0,07}} = 15,694)
O resultado anterior equivale a 188,33 meses
É oferecida a uma pessoa uma taxa de juros de forma que, se ela reinvestir mensalmente seu capital inicial, igual aos juros gerados; seu capital seria dobrado em 10 anos. Calcule a taxa de juros oferecida pelo banco e determine em quantos meses o principal será triplicado.
Solução: considere que 10 anos equivalem a 120 meses
Para resolver o problema, usaremos o modelo:
(Cleft( n right) = {C_0}{2^{frac{n}{{120}}}})
Note que para (n = 120:)
(Cleft( {120} right) = {C_0}{2^{frac{{120}}{{120}}}} = 2{C_0})
o que
({2^{frac{n}{{120}}}} = {left( {{2^{frac{1}{{120}}}}} right)^n})
Se tem
({2^{frac{1}{{120}}}} = 1,00579294 = 1 + 0,00579294)
Isso indica que a taxa mensal é (0,579294% ) ao mês, o que equivale a (12,070% ) ao ano.
Para saber em quantos meses triplicará, formularemos a equação:
(3{C_0} = {C_0}{2^{frac{n}{{120}}}})
(3 = {2^{frac{n}{{120}}}})
({log _2}3 = frac{n}{{120}}{log _2}2)
(n = 120left( {{{log }_2}3} right))
(n = 120left( {1.;5850} right) = 190,2)
Nota: Caso sua calculadora não tenha a opção de calcular ({log _2}3), você pode usar:
({log _b}c = frac{{{{log }_a}c}}{{{{log }_a}b}})
({log _2}3 = frac{{{{log }_{}}3}}{{{{log }_{}}2}})
Quantos anos tem uma figura de madeira que tem um terço de seu conteúdo original de carbono 14 se a meia-vida do material é de 5900 anos?
Solução: Para resolver o problema usaremos o modelo
(A = {A_0}{left( {frac{1}{2}} right)^{left( {frac{t}{{5900}}} right)}})
Onde: (A) é a quantidade de material no tempo t e ({A_0}) é o material inicial.
Quando (A = 0,14{A_0})
Você tem a equação:
(0.14{A_0} = {A_0}{left( {frac{1}{2}} right)^{left( {frac{t}{{5900}}} right)}})
(0,14 = {2^{ – frac{t}{{5900}}}})
({log _2}0,14 = – frac{t}{{5900}}{log _2}2)
({log _2}0,14 = – frac{t}{{5900}})
( – 2.;8365 = = – frac{t}{{5900}})
(t = left( { – 2.;8365} right)left( { – 5900} right))
(t = 16735)
Dada a base (b > 0,) diferente de 1, e o número (a > 0,;) podemos encontrar um número (t), tal que:
(a = {b^t},)
Nesse caso, diz-se que (t), é o logaritmo de (a) na base (b), o acima é denotado como:
(t = {log _b}a,)
imediatamente a igualdade é obtida:
(a = {b^t} = {b^{{{log }_b}a}},)
Quando a base (b = 10), os logaritmos são chamados de logaritmos decimais e para simplificar a seguinte notação é usada:
({log 10 }a = log a)
Tabela de logaritmos de base 2 das primeiras potências de dois.
| (a) | ({log _b}a) |
|---|---|
| (1 = {2^0}) | ({log _2}1 = 0) |
| (2 = {2^1}) | ({log _2}2 = 1) |
| (4 = {2^2}) | ({log _2}4 = 2) |
| (8 = {2^3}) | ({log _2}8 = 3) |
| (16 = {2^4}) | ({log _2}16 = 4) |
| (32 = {2^5}) | ({log _2}32 = 5) |
| (64 = {2^6}) | ({log _2}64 = 6) |
| (128 = {2^7}) | ({log _2}128 = 7) |
Tabela de logaritmos de base 2 das primeiras potências de um meio.
| (a) | ({log _b}a) |
|---|---|
| (0.5 = frac{1}{2}) | ({log _2}0,5 = – 1) |
| (0.25 = frac{1}{{{2^2}}}) | ({log _2}0,25 = – 2) |
| (0.125 = frac{1}{{{2^3}}}) | ({log _2}0,125 = – 3) |
| (0.0625 = frac{1}{{{2^4}}}) | ({log _2}0,0625 = – 4) |
| (0.03125 = frac{1}{{{2^5}}}) | ({log _2}0,03125 = – 5) |
| (0.015625 = frac{1}{{{2^6}}}) | ({log _2}0,015625 = – 6) |
O sistema decimal que utilizamos para escrever os números privilegia os logaritmos de base dez, por isso costumam ser os mais utilizados para os cálculos e para sua comodidade utiliza-se a seguinte convenção:
(log a = {rm{lo}}{{rm{g}}_{10}}a)
Tabela de logaritmos na base 10 das primeiras potências de 10.
| (a) | ({log _b}a) |
|---|---|
| (1 = {10^0}) | (log 1 = 0) |
| (10 = {10^1}) | (log 10 = 1) |
| (100 = {10^2}) | (log 100 = 2) |
| (1000 = {10^3}) | (log 1000 = 3) |
| (10000 = {10^4}) | (log 10000 = 4) |
| (100000 = {10^5}) | (log 100000 = 5) |
Tabela de logaritmos na base 10 das primeiras potências de um décimo.
| (a) | ({log _b}a) |
|---|---|
| (0.1 = {10^{ – 1}}) | ({rm{log;}}0,1 = – 1) |
| (0.01 = {10^{ – 2}}) | (log 0.01 = – 2) |
| (0,001 = {10^{ – 3}}) | (log 0,001 = – 3) |
| (0,0001 = {10^{ – 4}}) | (log 0,0001 = – 4) |
| (0,00001 = {10^{ – 5}}) | (log 0,00001 = – 5) |
| (0.000001 = {10^{ – 6}}) | (log 0,000001 = – 6) |
Em investigações de matemática e outros fenômenos da física, química, finanças, etc., é comum que o número de Euler apareça ( (e approx 2.718281828 ldots .;) ) elevado a uma potência e, portanto, é importante calcular logaritmos com base em (e,;) que são chamados de logaritmos naturais ((ln )) ou logaritmos naturais, para simplificar, temos a seguinte notação:
(ln a = {log _e}a.)
A partir das leis dos expoentes, estabelecem-se as seguintes propriedades dos logaritmos em uma base (b > 0):
({log _b}ac = {log _b}a + {log _b}c,)({log _b}frac{a}{c} = {log _b}a – { log _b}c,)({log _b}{a^n} = n{log _b}a.)
Nem todas as calculadoras de bolso podem calcular o logaritmo em qualquer base, mas se forem programadas para calcular logaritmos na base 10, as seguintes propriedades dos logaritmos permitem relacionar logaritmos em diferentes bases.
({log _b}a{log _a}b = 1,)({log _b}c = {log _a}c{log _b}a.)({log _b} c = frac{{{{log }_a}c}}{{{{log }_a}b}})
Da última igualdade, isolando ({log _b}a.) e substituindo-o em ({log _b}c = {log _a}c{log _b}a,) resulta:
({log _b}c = frac{{{{log }_a}c}}{{{{log }_a}b}})
A função exponencial e a função logarítmica estão fortemente relacionadas. De fato, temos as seguintes relações:
({log _b}{b^x} = x,)
({b^{{{log }_b}x}} = x.)
Vamos analisar o caso quando (a > 1:)
Neste caso já sabemos que se (p > q,) então: ({a^p} > {a^q};;)
Seja (0 < x < 1;) tal que ({a^0} = 1,;) consequentemente, ({rm{lo}}{{rm{g}}_a}x < 0.)
Seja (1 < x < a;) tal que ({a^1} = a,;) consequentemente, (0 < {rm{lo}}{{rm{g}}_a } x < 1.)
Seja (a < x;) tal que ({a^1} = a,;) consequentemente, (1 1), é mostrado abaixo
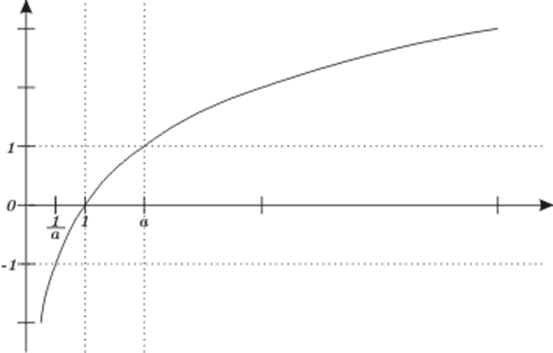
Gráfico de ({log _a}x) quando (a > 1)
Vamos analisar o caso quando (0 < a q,) então: ({a^p} < {a^q};;)
Seja (0 < x 1. )
Seja (a < x < 1;) tal que ({a^1} = a < x < {a^0}) então (0 < {rm{lo}}{{rm{ g} }_a}x < .1)
Seja (1 < x;) tal que ({a^0} = a,;) então ({rm{lo}}{{rm{g}}_a}x < 0. )
O gráfico do logaritmo para a base (a), quando (a < 1), é mostrado abaixo
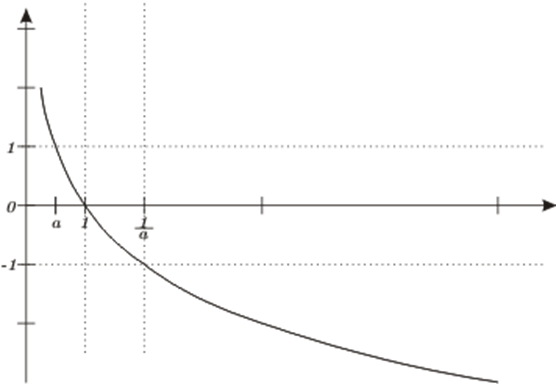
Gráfico de ({log _a}x) quando (a < 1)

Artigo de: Marco Antonio Rodríguez Andrade. Graduado em Física e Matemática, com mestrado em Matemática, ambos pela ESFM, e doutorado em Ciências pela UNAM.
Referencia autoral (APA): Rodríguez Andrade, M. A.. (Dez. 2022). Conceito de Logaritmo. Editora Conceitos. Em https://conceitos.com/logaritmo/. São Paulo, Brasil.