
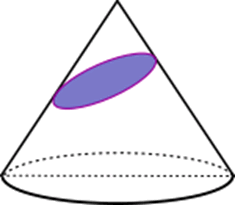
A elipse é uma das cônicas estudadas desde a época dos gregos, sobre a referência de Apolônio, que tem sido útil para explicar a trajetória dos planetas e no desenho de salas com características acústicas excepcionais. Quando um cone reto é interceptado por um plano nem paralelo à geratriz do cone nem perpendicular à sua base, o resultado é uma Elipse. Quando o plano é paralelo forma-se um círculo e este caso merece tratamento especial.
Dados dois pontos fixos \({F_1}\) e \({F_2}\), que chamaremos de Focos da Elipse e uma constante \(k > 0\); a Elipse com focos nos pontos \({F_1}\) e \({F_2}\), é o lugar geométrico dos pontos do plano cujas distâncias aos pontos \({F_1}\) e \({F_2 } \) é igual a uma constante \(k\), ou seja:
\(P{F_1} + P{F_2} = k\)
Dados dois pontos fixos \({F_1}\) , \({F_2}\) e uma constante \(k > 0\) podemos construir vários pontos que pertencem à elipse que satisfaz:
\(P{F_1} + P{F_2} = k;\)
Para fazer isso, basta realizar as seguintes etapas.
Situação inicial
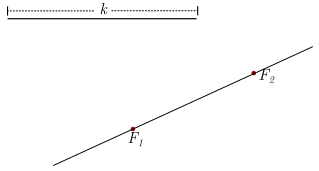
No ponto \({F_1}\) é traçado um arco de raio \({a_1}\) (verde) e no \({F_2}\) um círculo de raio \(k – {a_1}\) (azul ). As interseções destes arcos são marcadas, neste caso \({P_1}\) e \(P_1^\prime\).
A forma como os raios foram escolhidos é garantida:
\({F_1}{P_1} + {F_2}{P_1} = k\)
\({F_1}P{^\prime_1} + {F_2}P{^\prime_1} = k\)
No ponto \({F_2}\) é traçado um arco de raio \({a_1}\) (verde) e no \({F_1}\) um círculo de raio \(k – {a_1}\) (azul ). As interseções desses arcos são marcadas, neste caso \({Q_1}\) e \(Q_1^\prime\)
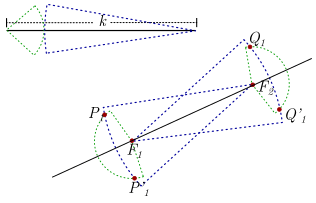
No ponto \({F_1}\) é traçado um arco de raio \({a_2}\) (verde) e no \({F_2}\) um círculo de raio \(k – {a_2}\) (azul ). As interseções destes arcos são marcadas, neste caso \({P_2}\) e \(P_2^\prime\).
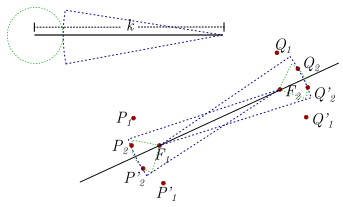
A forma como os raios foram escolhidos é garantida:
\({F_1}{P_2} + {F_2}{P_2} = k\)
\({F_1}P{^\prime_2} + {F_2}P{^\prime_3} = k\)
No ponto \({F_2}\) é traçado um arco de raio \({a_2}\) (verde) e no \({F_1}\) um círculo de raio \(k – {a_2}\) (azul ). As interseções desses arcos são marcadas, neste caso \({Q_2}\) e \(Q_2^\prime\)
Da mesma forma, mais pontos são construídos.
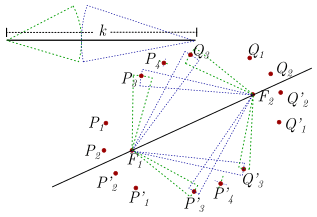
Unindo os pontos, obtém-se o contorno de uma elipse cujos focos são os pontos \({F_1}\) e \({F_2}.\)
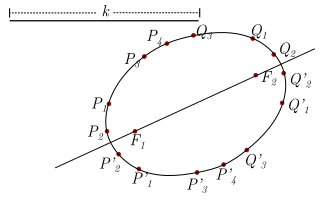
A figura a seguir mostra outros elementos importantes da elipse.
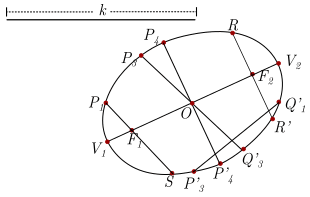
| Elemento | Descrição | Exemplo |
|---|---|---|
| Centro da Elipse | O ponto médio do segmento \(\overline {{F_1}{F_2}} \), onde \({F_1}\) e \({F_2}\) são os focos da elipse. | \(O\) |
| Eixo focal ou eixo principal | É a linha que passa pelos focos | |
| Vértice da elipse | Interseção do eixo focal com a elipse | \({V_1}\) e \({V_2}\) |
| Eixo conjugado ou eixo menor | Segmento de linha que une dois pontos da elipse | |
| Sequência | Segmento de linha que une dois pontos da elipse | \(\overline {P_3^\prime Q_1^\prime } \) |
| Cordão Focal | Corda passando por um dos focos da elipse | \(\overline {{P_1}S} \) |
| Lado Reto | Corda focal perpendicular ao eixo focal | \(\overline {RR^\prime } \) |
| Diâmetro da elipse | Corda passando pelo centro | \(\overline {{P_1}P_3^\prime } \) |
Características da elipse
A elipse tem dois eixos de simetria, a saber: o eixo focal e o eixo conjugado que denotaremos como
\(a = O{V_1},\)\(b = OP\)\(c = O{F_1}\)

| Elemento | Descrição | Valor |
|---|---|---|
| Semi-eixo maior | Comprimento do segmento \(\overline {O{V_1}} \) | \(a\) |
| Semi-eixo menor | Comprimento do segmento \(\overline {OQ} \) | \(b\) |
| Eixo principal | Comprimento do segmento \(\overline {{V_1}{V_2}} \) | \(2a\) |
| Eixo menor | Comprimento do segmento \(\overline {QQ’} \) | \(2b\) |
| Distância focal | Comprimento do segmento \(\overline {{F_1}{F_2}} \) | 2\(c\) |
Eles têm o seguinte:
\(k = 2a\)
Quer dizer:
\(P{F_1} + P{F_2} = k = 2a,\;\)
Pelo teorema de Pitágoras:
\({b^2} + {c^2} = {a^2}.\)
Uma forma de desenhar uma elipse em um programa de desenho é determinar a localização do centro e os valores dos eixos maior e menor, não sendo necessário indicar a posição de cada um dos focos da elipse; que pode ser determinado usando a relação:
\({b^2} + {c^2} = {a^2}.\)
Por exemplo, se uma elipse é desenhada em um programa de desenho cujos eixos medem 6cm e 10cm, então os semi-eixos medem 3cm e 5cm; e a distância focal pode ser calculada da seguinte forma:
\({3^2} + {c^2} = {5^2}\)
Resolvendo a equação, obtém-se que a distância focal é de 4 cm.
Dados dois pontos fixos \({F_1}\) e \({F_2}\), que chamaremos de Focos da Elipse e uma constante \(a > 0\); a Elipse com focos nos pontos \({F_1}\) e \({F_2}\), é o lugar geométrico dos pontos do plano cujas distâncias aos pontos \({F_1}\) e \({F_2 } \) é igual a uma constante \(k\), ou seja:
\(P{F_1} + P{F_2} = 2a\)
Equações da elipse com centro na origem e eixo focal em um dos eixos coordenados
Posição da elipse
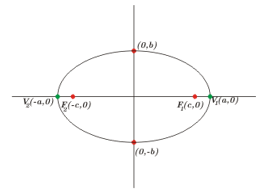
Centro em \(\left( {0,0} \right).\) Focos em \({F_1}\left( { – c,0} \right),\;{F_2}\left( {c,0 } \right).\) Vértices em \({V_1}\left( { – a,0} \right),\;{V_2}\left( {a,0} \right).\;\)Eixo Focal : eixo X\)
Equação da parábola
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Onde é cumprido:
\({b^2} + {c^2} = {a^2}.\)
Posição da elipse
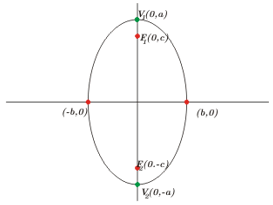
Centro em \(\left( {0,0} \right).\) Focos em \({F_1}\left( {0, – c} \right),\;{F_2}\left( {0,c } \right).\) Vértices em \({V_1}\left( {0, – a} \right),\;{V_2}\left( {0,a} \right).\;\)Eixo Focal Eixo y\)
Equação da parábola
\(\frac{{{x^2}}}{{{b^2}}} + \frac{{{y^2}}}{{{a^2}}} = 1\)
Onde é cumprido:
\({b^2} + {c^2} = {a^2}\)
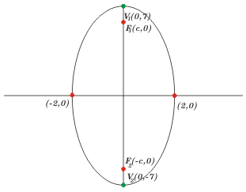
O eixo focal está no eixo de ordenadas (o eixo \(y\)) seus semi-eixos medem 7 e 2 respectivamente e seu centro está na origem
Equação da elipse
Neste caso
\(a = 7,\;b = 2,\) portanto
\(c = \sqrt {{7^2} – {2^2}} = \sqrt {45} = \sqrt {{3^2}5} = 3\sqrt 5 \)
\(\frac{{{x^2}}}{{{b^2}}} + \frac{{{y^2}}}{{{a^2}}} = 1\)
\(\frac{{{x^2}}}{{{2^2}}} + \frac{{{y^2}}}{{{7^2}}} = 1\)
\(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{{49}} = 1\)
Esboço do gráfico
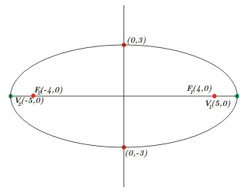
O eixo focal está no eixo das abcissas (eixo \(x\)), sua distância focal mede 8, seu eixo maior mede 10 e seu centro está na origem
Equação da elipse
Neste caso
\(a = 4,\;c = 5,\) portanto
\(b = \sqrt {{5^2} – {4^2}} = \sqrt 9 = 3\)
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
\(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
\(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Esboço do gráfico
Posição da elipse
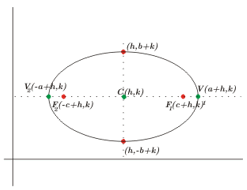
Centro em \(\left( {h,k} \right).\) Focos en \({F_1}\left( {h – c,k} \right),\;{F_2}\left( {h + c,k} \right).\) Vértices en \({V_1}\left( {h – a,k} \right),\;{V_2}\left( {h + a,k} \right).\;\) Eixo Focal: \(y = k\)
Equação da elipse
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{b^2}}} = 1\)
Onde é cumprido:
\({b^2} + {c^2} = {a^2}.\)
Posição da elipse
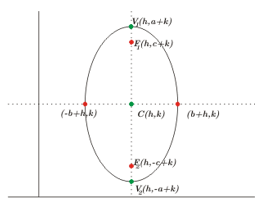
Centro em \(\left( {h,k} \right).\) Focos em \({F_1}\left( {h,k – c} \right),\;{F_2}\left( {h, k + c} \right).\) Vértices em \({V_1}\left( {h,k – a} \right),\;{V_2}\left( {h,k + a} \right). \;\)Eixo Focal \(x = h\)
Equação da elipse
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{b^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{a^2}}} = 1\)
Onde é cumprido:
\({b^2} + {c^2} = {a^2}\)
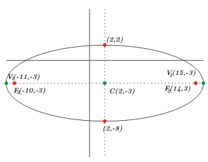
Os focos são \({F_1}\left( { – 10, – 3} \right),\;{F_2}\left( {14, – 3} \right)\) e seu eixo maior é igual a 26.
Equação da elipse
Neste caso: \(2c = {F_1}{F_2} = 24,\) portanto: \(c = 12\)
\(2a = 26\)
\(a = 13\)
\({b^2} + {c^2} = {a^2}\)
\({b^2} + {12^2} = {13^2}\)
\({b^2} = {13^2} – {12^2}\)
\({b^2} = 25\)
O centro da elipse está no ponto médio do segmento \(\overline {{F_1}{F_2}} \) que é \(C\left( {2, – 3} \right).\)
O eixo focal é paralelo ao eixo \(x\).
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{b^2}}} = 1\)
\(\frac{{{{\left( {x – 2} \right)}^2}}}{{{{13}^2}}} + \frac{{{{\left( {y – \left( { – 3} \right)} \right)}^2}}}{{{5^2}}} = 1\)
\(\frac{{{{\left( {x – 2} \right)}^2}}}{{25}} + \frac{{{{\left( {y + 3)} \right)}^2}}}{{169}} = 1\)
Gráfico de esboço
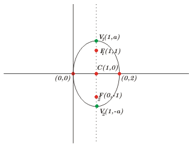
Os focos são \({F_1}\left( {1,1} \right),\;{F_2}\left( {1, – 1} \right)\) e seu eixo menor é igual a 2.
Equação da elipse
Neste caso: \(2c = {F_1}{F_2} = 2,\) portanto: \(c = 1.\)
\(2b = 2\)
\(b = 1\)
\({b^2} + {c^2} = {a^2}\)
\({1^2} + {1^2} = {a^2}\)
\(2 = {a^2}\)
O centro da elipse está no ponto médio do segmento \(\overline {{F_1}{F_2}} \) que é \(C\left( {1,0} \right).\)
O eixo focal é paralelo ao eixo das \(y\).
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{b^2}}} = 1\)
\(\frac{{{{\left( {x – 0} \right)}^2}}}{2} + \frac{{{{\left( {y – 1)} \right)}^2}}}{{{1^2}}} = 1\)
\(\frac{{{x^2}}}{2} + {\left( {y – 1} \right)^2} = 1\)
Esboço do gráfico

Artigo de: Marco Antonio Rodríguez Andrade. Graduado em Física e Matemática, com mestrado em Matemática, ambos pela ESFM, e doutorado em Ciências pela UNAM.
Referencia autoral (APA): Rodríguez Andrade, M. A.. (Março 2023). Conceito de Elipse. Editora Conceitos. Em https://conceitos.com/elipse/. São Paulo, Brasil.